Geometry: From Euclid to Escher


Professor Maciej Dunajski is a Fellow of Clare and a Professor of Mathematical Physics at the Department of Applied Mathematics and Theoretical Physics at the University of Cambridge. His research interests are Differential and Projective Geometry, Solitons, and General Theory of Relativity. In 2021 he was awarded the Atiyah Fellowship by the London Mathematical Society.
The Fellows’ Library holds several copies of the Elements by Euclid of Alexandria, including the 1620 edition donated by Robert Greene*, a Fellow of the College from 1703 to 1730.
The Elements is regarded as one of the most influential books of all times, and is surpassed only by the Bible in the number of editions published. Although the text goes back to the 3rd century BCE, it has until relatively recently been used for teaching geometry at high school and university levels. Imagine teaching biology or physics from a source of similar age. In these fields, anything written more than 50 years ago is regarded as outdated, and often wrong. This is because the science is moving forward. Geometry is also moving forward, but once a correct proof of a theorem has been presented, it becomes timeless.
Geometry - in the ancient Greek geo means earth, and metron means measurement - is a branch of mathematics concerned with distances, shapes and areas. It stands out from other areas of mathematics in that a proof of a theorem can be given in pictorial terms, without a need for algebra or mathematical symbols, and without sacrificing rigour. The Pythagorean theorem is a good example. It states that for any right-angled triangle the square of the hypotenuse c is equal to the sum of the squares of the other two sides a and b (Figure 2).

Figure 1: Euclid’s Elements of Geometry.
Figure 1: Euclid’s Elements of Geometry.
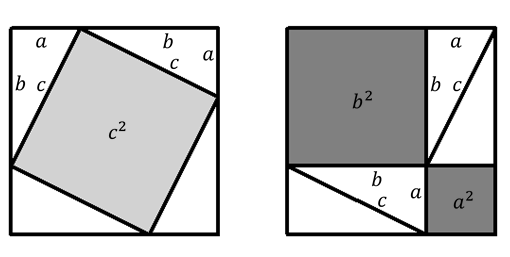
Figure 3: A proof of the Pythagorean theorem.
Figure 3: A proof of the Pythagorean theorem.
*Greene was a scientific eccentric who aspired to the fame of Newton, wrote a treatise on squaring the circle, and asked in his will for his skeleton to be hung in King’s College library. I thank Tim Chesters and Catherine Reid for bringing this character to my attention.
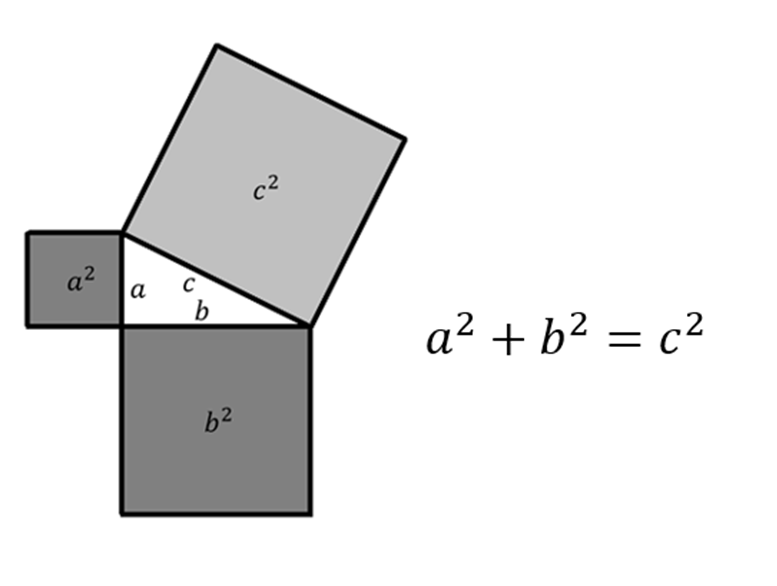
Figure 2: The Pythagorean theorem.
Figure 2: The Pythagorean theorem.
One of the many proofs of the Pythagorean theorem is given in Figure 3.
While it may take some explaining to convince you that all the triangles in the left hand square can be rearranged to those in the right hand one, the proof is essentially self-contained. In fact the concept of a mathematical proof - deductive reasoning from a set of axioms - first arose in geometry.
The ancient Egyptians and Mesopotamians engaged with geometry before the Greeks did, but primarily for practical reasons. Thus a line segment connecting two points could have meant a piece of string between two pegs in the sand, or a straight path between two villages. It was the Greeks who made geometry abstract, and axiomatic. Axioms are statements which are evidently true. In geometry they were listed by Euclid who, starting from intuitively clear building blocks like points and lines, made an attempt to put geometry in a logical framework.
Axiom 1 Exactly one straight line segment may be drawn between any two points.
Axiom 2 A straight line segment may be extended indefinitely.
Axiom 3 A circle may be drawn with any given centre and an arbitrary radius.
Axiom 4 All right angles are equal.
Axiom 5 (The parallel postulate) Given a line l and a point P not on l, there is exactly one line which contains P, and does not intersect l (Figure 4).
Using these axioms, Euclid and his followers could arrive at theorems which are logical consequences of axioms.
How can we be sure that some of Euclid’s five axioms are not in fact theorems, which can be deduced from a smaller set of axioms? For over two millennia it had been suspected that Euclid’s fifth axiom - the parallel postulate - could be deduced from the first four. The matter was put to a close in the 19th century by Nikolai Lobachevsky, Janos Bolyai and Carl Friedrich Gauss, who gave an example of a non–Euclidean geometry consistent with the first four axioms. In this example, which now bears the name of hyperbolic geometry, the parallel axiom, however, does not hold.
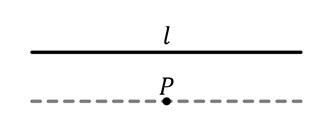
Figure 4: The parallel postulate.
Figure 4: The parallel postulate.
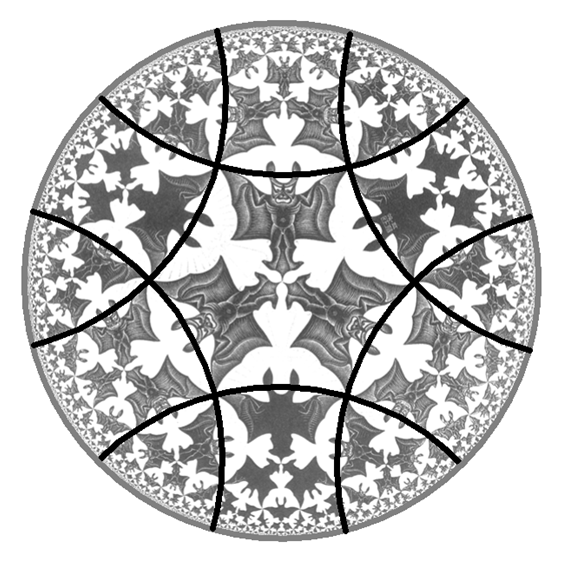
Figure 5: Escher’s Circle LimitIV. A model of hyperbolic geometry.
Figure 5: Escher’s Circle LimitIV. A model of hyperbolic geometry.
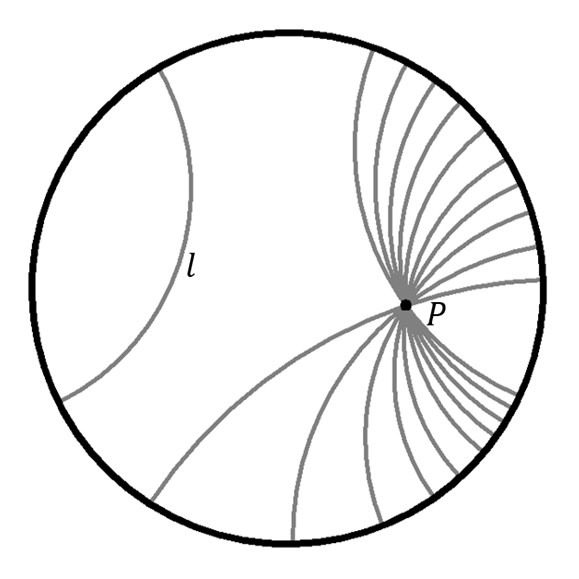
Figure 6: Infinitely many parallel lines.
Figure 6: Infinitely many parallel lines.
The arena for hyperbolic geometry is a disc: the interior of a circle. The 20th century Dutch artist M. C. Escher represented this geometry on such a disc tiled with infinitely many angels and devils. Points on the boundary are infinitely far apart - the notion of the distance is distorted in hyperbolic geometry. The analogues of straight lines are diameters of the bounding circle, and circular arcs intersecting this boundary at right angles. Six such arcs have been drawn on Figure 5. The arcs and diameters are called the hyperbolic lines, and any two points inside the disc can be connected by a unique hyperbolic line.
Given a hyperbolic line l, and a point P inside the disc, and not on this line, there are infinitely many hyperbolic lines through P which do not intersect l. These hyperbolic lines are therefore parallel to l, and some of them are shown on Figure 6. This shows that hyperbolic geometry, while obeying the first four of Euclid’s axioms, violates the fifth one. It is therefore impossible to deduce Euclid’s parallel axiom from the first four, for if it could be deduced, then it would also hold in hyperbolic geometry, which is not true.
The devils close to the boundary circle in Figure 5 appear smaller than those near the centre of the disc, but the hyperbolic area and height of each devil from head to tail are the same when hyperbolic distance, rather than Euclidean distance, is used. All the devils, even those which appear close to the boundary from the Euclidean perspective, are actually infinitely far from the boundary circle. It may seem to us that the devils reside inside a circle, but for them there is no ‘outside’, as the circle is infinitely large from a hyperbolic perspective. We have been fooled by our Euclidean intuition!
References
[1] The Thirteen Books of Euclid’s Elements, translation and commentaries by Thomas Heath, (1956) Dover Publications.
[2] M.C. Escher: The Graphic Work. M.C. Escher and Bruce Brooks Pfeiffer (Editor). (2001) Taschen.
[3] Geometry: A Very Short Introduction. M. Dunajski, (2022). Oxford University Press.